Sacred Geometry in Nature
Sacred geometry is the nexus point between physics and mysticism. It is the realm where infinities live within finite forms, and the chaos of creation is brought to order.
The true beauty of sacred geometry is that it satisfies both the right and left brain. Elegant expressions of compelling proportional relationships simultaneously activate the intellectual and artistic functions, merging the rational with the abstract.
Sacred geometry arises from the desire to express philosophical truths through concrete means. It offers a scientific method for philosophical inquiry, complete with hypotheses, experiments, and repeatable results.
The best way to study the fundamental shapes of nature is to draw them yourself. In order to fully appreciate this article, I would encourage you to procure paper, pencil, compass and straight edge in order to perform at home the experiments here described.
Now, we will embark on a journey through creation as it arises in spheres, lines, and spirals. Fair warning: visceral engagement with these shapes can be irrationally rewarding; what begins as strictly formulaic may soon become more magical than ever expected.
Geometry as Nature’s Language
Geometry is not merely symbolic. It is nature’s way of solving problems with elegance and efficiency. The spiral of a galaxy mirrors the curl of a seashell, the hexagon of a honeycomb repeats in basalt columns, and the fractal branching of trees resembles lightning, rivers, and lungs. These recurring shapes reveal that nature builds through balance, proportion, and repetition.
In this sense, sacred geometry is also natural geometry, the mathematical language of creation itself. Patterns like the Fibonacci sequence and Golden Ratio govern growth and form, producing harmony in seashells, flowers, and snowflakes alike. Whether viewed through physics or philosophy, these patterns show that geometry connects all things, linking matter, energy, and consciousness through timeless order.
Seed, Flower, Fruit
By way of introduction, let us consider the life cycle of any fruit-bearing tree. Down from the ancestors, a seed reaches Earth, is buried, and germinates. Its cells divide, and the seed expands into a baby plant. A stable trunk grows up, and the tree eventually flowers, portending abundant fruits to come. When ripe, a fraction of the fruits fall to the earth. The flesh rots into compost that then feeds the new seeds now underground, just waiting for the day when the process starts anew.
This cycle ought to be painfully familiar to anyone with even the briefest human experience. Like plants, people are born, grow up, bear fruit, decay, and then die in order to feed that which is being born. This exact pattern is mirrored by the most fundamental processes of sacred geometry. In many ways, sacred geometry mirrors nature’s own mathematics. Every stage of growth, from seed to bloom, follows proportion and symmetry, the same structure seen in galaxies, shells, pinecones, and petals. Geometry turns chaos into harmony, forming a bridge between energy and matter.
The Geometry of Beginnings
Our journey begins with a single circle, which may also be drawn or imagined as a sphere. This is not yet a seed, but its mere potential. This first circle is an abstract concept that serves as the perpetual center point and container for all that comes next. If you are drawing along, this is a good time to bust out your compass and draw a circle — probably smaller than you might initially like — in the center of your paper.
The first movement on the road to fruition is duplication. Keeping the compass set to precisely the same radius, place its point anywhere along the circumference of the first circle and draw a second circle so that its edge passes through the center point of the first. You are now looking at a shape known as vesica piscis, the womb of creation, or literally, “the bladder of a fish.” This shape represents the union of opposites, the resolution of polarity. Two distinct entities overlap to create a unified space wherein a distinct third entity can arise. Need I explain why this shape is associated with femininity?
The vesica piscis also represents balance and proportion—the same mathematical harmony seen in natural systems. Its shape reflects the Golden Ratio (1.618), a universal constant appearing in countless living forms. These connections reveal that geometry doesn’t just symbolize creation—it describes how nature organizes itself. Consider where these relationships appear:
- Flower petals and seed patterns often follow Fibonacci spacing, optimizing light and space.
- Seashells and hurricanes form logarithmic spirals based on predictable geometric ratios.
- Cell division and water ripples recreate vesica-like intersections, showing how life literally builds from geometric relationships.
The Seed of Life and Cosmic Patterns
Here we have all the information needed to generate two equilateral triangles within the “womb,” where the circles overlap. Draw a line connecting the center points of the two circles. Now connect each center point directly to the point where the circles cross paths. You now have two equilateral triangles on either side of a horizontal (x) and an implied vertical (y) axis. From here, we can infer the existence of six equidistant points around one of the circles. A protractor is a useful tool to maintain precise measurements at this juncture, although a straight-edge is sufficient, and ultimately, a compass is all you need.
Now then, place the point of the compass on each of these new points and draw five more circles. You are now looking at something like this: This conglomeration of circles is called the Seed of Life. When someone mentions sacred geometry, the Seed arises first in my mind’s eye. It is extremely common to see derivations of this structure in visionary art, corporate logos, and new age tattoos.
Despite its pervasive usage, the shape is so fundamental to the structure of the cosmos that humans will never grow weary of its perfect harmonics. Would you or anyone deny that this pattern is infinitely pleasing? It is so interwoven into our lives that we may not even notice the depth of its symbolism. Where else do we encounter the concept of six encircling one?
The days of the week come to mind, based as they are upon the six days of creation, followed by a single day of rest. Similarly, there are six heavenly bodies (Mercury, Venus, Moon, Mars, Jupiter, Saturn) visible to the naked eye, all encircling the central sun. In addition, many traditions identify seven chakras, where the heart-center is encircled by three upper and three lower chakras. Likewise, there are seven perceptible colors in the rainbow, with green at the center and red or violet at either end of the spectrum.
There are plenty more of these examples available if you care to investigate further on your own, but evolution is ongoing, and so are we. These examples remind us that geometry acts as nature’s blueprint. Symmetry, proportion, and cycles repeat across every scale, from atomic bonds to planetary motion. The same geometry that governs sacred art also guides how trees branch, rivers divide, and clouds swirl.
Geometry as the Framework of Creation
Geometry is the silent architect of the natural world. From the symmetry of a snowflake to the balance of a pinecone’s spiral, it defines how energy finds equilibrium through structure.
- Symmetry ensures balance and stability in living and nonliving systems.
- Proportion determines harmony, appearing in everything from DNA strands to flower petals.
- Repetition creates fractal continuity, building infinite complexity from simple rules.
- The Golden Ratio serves as a universal guide for beauty, efficiency, and structural integrity.
Sacred geometry gives language to these invisible laws, revealing how creation reflects mathematical truth. It unites science and spirituality, showing that everything—from seeds to stars—follows the same sacred pattern of order, rhythm, and renewal.
From Seed to Flower
Once germinated, the seed becomes a plant and achieves its utmost beauty in the form of a flower. In sacred geometry, this is shown by adding another ring of six circles around the Seed, so that we now have twelve encircling one.
Just as a plant’s growth follows a predictable rhythm, geometry guides this unfolding process in nature. Circles, spirals, and hexagons emerge because they’re the most efficient ways for life to grow and organize itself. These same patterns form the foundation of sacred geometry, reflecting how mathematical order shapes both natural and spiritual creation.
(Remember: you can always add a circle around the outside to contain the entire shape. Just like the infinitesimally tiny dot at the very center, it doesn’t influence the overall energetics of the form.)
Is this a familiar shape? Does it have any applications in nature or human culture?
Common examples include the twelve signs of the zodiac that encircle our perspective here on Earth and the twelve hour-markers on the face of a clock. The famous Jesus of Nazareth is said to have had twelve disciples, the same way King Arthur led the twelve knights of the Round Table. We recognize twelve months in a year, and there is often a thirteenth full moon hidden within those solar months.
According to John Michell in How the World is Made, twelve “is the root number in the code of proportions that governs the solar system… In some remote, unknown age, the zodiac was divided into twelve sections so that the sun passed through one zodiacal house or sign in 2160 years, which is… the same as the diameter of the moon in miles…”
Far beyond any possibility of coincidence, such alignments reveal the divine intelligence inherent to creation. Such mysterious rationality and beautiful order cannot be the result of so many mere happy accidents.
This same harmony appears throughout nature’s geometry, revealing how creation balances beauty with efficiency:
- Spirals unfold in ferns, pinecones, and galaxies, expanding infinitely while maintaining proportion.
- Hexagons form in honeycombs and snowflakes, filling space with perfect precision.
- Fractals repeat in trees, rivers, coral, and lightning, demonstrating how complexity arises from simple repetition.
These forms remind us that sacred geometry is not confined to ancient symbols. It’s visible in every leaf, seashell, and snowflake, linking mathematical design to life’s ongoing evolution.
The fact that the Flower of Life is found carved or otherwise encoded into the remnants of ancient civilizations the world over only adds to the power of this image to inspire us toward further study of the fixed forms that give rise to reality as we know it.
Metatron’s Cube
In any healthy organism, flowering precedes the production of fruit. After the flower expresses its irrepressible beauty and fragrance, it wilts and all that energy redirects to generate the next generation.
Plants are super intelligent but basically immobile. As such, they have strategies to spread their seeds. Primary among these is to hide seeds within a delicious morsel so that some animal might pass by, consume the fruit and in its droppings, drop the seed in a far off the fertile ground. Thus the species is propagated, arriving in fresh territory already encased in the best kind of compost.
The fruit of one’s labor, loins, or karma refers to the tangible output of a period of incubation; to the cumulative and far-reaching effect of a collection of causes.
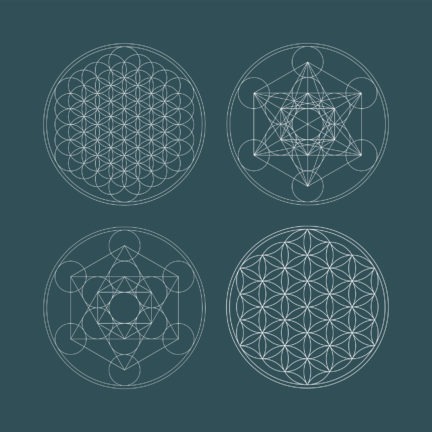
Metatrons Cube and Flower of life.
The fruit is the distillation of all previous efforts and growth. That which has been expanding now sheds superfluous forms to become highly concentrated in order to create new forms. To obtain excellent fruits, one must prune the tree.
The glorious complexity of the Flower is reduced in order to produce the Fruit of Life. This little death serves that which is being born.
Now simplified, the Fruit becomes the creative framework from which the infinite potential of Metatron’s Cube springs to life.
Home Geometers, if you haven’t already, draw a fresh Fruit of Life, separate from your other scribbles. Use a new paper if need-be.
Now, connect the center points of the thirteen circles that compose the Fruit, and you’ll discover a web of interlocking lines that are the two-dimensional representation of the three-dimensional polyhedra that are the complete structural basis for human experience. This multidimensional shape-stack is called Metatron’s Cube.
Esoterically, Metatron is an archangel, one of the energetic entities that oversee our particular corner of creation. Among the archangels, Metatron is understood to be the architect, the transcendent genius of shape and proportion. Metatron governs the specific logistics by which consciousness is able to take form.
Dear reader, at our shared level of experience, the most fundamental forms we can grasp are the five Platonic solids. The tetrahedron, octahedron, cube, icosahedron, and dodecahedron are the building blocks of our reality. These polyhedra are the only shapes in existence that have uniform numbers of sides, side lengths, and internal angles. They are the only perfectly symmetrical three-dimensional forms possible.
The five Platonic Solids correspond to the five elements and our five senses; they define the relationships between planetary orbits and atomic structures; they are the tools of Metatron; they are the vehicle whereby the Many arise from the One. The Platonic solids are the primary focus of a different article on the Gaia network.
Two Kinds of Spirals
If you’ve drawn along with us this long, congratulations — you have now sketched an outline of everything that is or could be. There is, however, one more dynamic we must acknowledge before reaching completion, and that is the quality of spin.
At each successive stage in the evolution from seed to flower, we simply added one more ring of circles around the center. This linear style of the spiral is called Archimedean, after the great Archimedes of Syracuse.
Archimedean spirals progress in a linear fashion, the way paper towel is wrapped around cardboard, or a rope is a coiled layer by layer. This is contrasted to a Phi, or Golden spiral, which expands proportionally according to the Fibonacci sequence. The Phi spiral is in fact far more common in nature, observable in phenomena such as whirlpools, tornadoes and spiral galaxies.
An excellent exercise to experience the difference between these two types of spirals is given on page 120 of A Beginner’s Guide to Constructing the Universe, by Michael Schneider.
In essence, the instructions are to cut two strips of paper and decide on a unit of measurement (inches, finger-breadths, it doesn’t matter). Beginning at one end of the first strip, measure and mark units of sequentially increasing value (1, 2, 3, 4…). For example, if the first section is one inch, then the second section is two inches, and so on. Then fold a right angle at each mark on this strip, and feel an Archimedean spiral unfold in your very own hands.
Do the same thing with the second strip of paper, except that here the length of each section is determined by the Fibonacci sequence (1, 1, 2, 3, 5, 8, 13…). Again, make a right angle at each mark and compare the results. When finished, you’ll have earned a direct and profound understanding of the two types of spirals that exist in nature.
Traces of the Creator
This essay tracks the organic evolution of potential energy into actuality using the simplest shapes available. These are the building blocks of sacred geometry.
These are concrete representations of abstract, otherwise inconceivable ideas. Simple shapes, lines, and curls generate a journey through the dimensions, perpetually approaching zero or infinity, the One and Many.
To discern the patterns by which creation unfolds and retracts is to approach the Creator directly. By participating in the process yourself, literally tracing the steps of the Creator, you have initiated yourself into a mystery tradition whose only limits are your own imagination.
This is truly universal knowledge, and according to Drunvalo Melchizedek, “It’s outside of any race or religion. It is a pattern that is intimately part of nature. If you go to distant planets where there is consciousness, I’m sure you’ll find the same image.”
Go on, then!
About the Author
All About the Infinity Symbol and Its Spiritual Meaning
The infinity symbol (∞) is a figure that appears simple at first glance, yet it is deeply charged with spiritual and energetic meaning. It represents continuous flow, the balance of opposites, and the eternity of existence. In this article, we explore what the infinity symbol is, its role in sacred geometry, and how to integrate it into spiritual practices to connect with the eternal cycle of consciousness.
Table of Contents
- What Is the Infinity Symbol and What Does It Represent Spiritually?
- Symbolic Structure of the Infinity: Eternal Loop and Balance
- The Infinity Symbol in Sacred Geometry
- Origin and Use of the Infinity Symbol in Different Traditions
- The Power of the Infinity Symbol in the Expansion of Consciousness
- How to Use the Infinity Symbol in Spiritual Practices
- Differences Between the Infinity Symbol and Other Sacred Symbols
What Is the Infinity Symbol and What Does It Represent Spiritually?
The infinity symbol is formed by a continuous curve that crosses at the center, creating two symmetrical loops. Its shape suggests perpetual movement, without beginning or end, making it a reminder of the eternal cycle of life and the interconnection of everything that exists. Over time, this symbol has been adopted as a representation of balance, expansion, and energetic continuity.
From a spiritual perspective, this symbol expresses the idea of unity within duality. Each loop represents opposing aspects—such as masculine and feminine, body and soul, giving and receiving—that find balance at a central point. It is attributed with the ability to reflect the soul’s journey through time, continuous learning, and the limitless expansion of consciousness.
Symbolic Structure of the Infinity: Eternal Loop and Balance
The shape of the infinity symbol is composed of a single curved line that intertwines at its center, generating two identical lobes. This structure represents an uninterrupted flow of energy that moves in cycles, reminding us that everything that begins eventually returns to its origin. The central crossing point symbolizes dynamic balance between polarities.
Each half of the symbol reflects an opposing yet complementary force, such as light and shadow, action and contemplation, expansion and contraction. When they meet at the center, both energies integrate into a single harmonious movement. This integration is key on the spiritual path, where inner balance allows the transcendence of duality.
The continuous line also represents the eternity of the soul and its connection with the whole. By having no beginning or end, the symbol invites us to understand existence as an uninterrupted process, where each experience is part of a greater cycle. For this reason, its structure is associated with the essential unity of all things and with the awareness that everything is in constant transformation.
The Infinity Symbol in Sacred Geometry
Within Sacred Geometry, the infinity symbol is recognized as a graphic expression of the universal flow of energy. Although it is not part of the Platonic solids or figures composed of polygons, its curved structure connects it with patterns of movement that repeat in nature and throughout the cosmos. For this reason, it is considered an energetic figure rather than a structural one.
This symbol is directly related to the concept of vibratory continuity and resonance. Its fluid movement represents how energy is transmitted without interruption through the different levels of existence. For that reason, it is used as a visual guide in meditative practices, helping to align the energy body with the rhythm of the universe.
In the series Sacred Geometry: Spiritual Science, available on Gaia, it is explained how figures such as the infinity symbol act as bridges between human perception and the hidden laws of the cosmos. Through visualizations and practical teachings, it explores how this shape can be used to activate expanded states of consciousness and connect with the universal order that sustains life.
Origin and Use of the Infinity Symbol in Different Traditions
Although the infinity symbol as we know it today became popular in modern times, its essence is found in spiritual traditions from different cultures. In Ancient Egypt, interwoven serpent figures were used to represent cycles of renewal and eternity—an idea that would later be reflected in the infinity symbol. In pre-Columbian cultures as well, certain circular and spiral patterns expressed the uninterrupted connection between time, nature, and spirit.
In Eastern philosophy, the cyclical flow of the infinity symbol resonates with concepts like yin and yang, where opposing forces complement each other in a constant dance of balance. This vision of eternal movement is present in disciplines such as Taoism, which sees life as a path without beginning or end, where everything returns to its source. Energy flowing without interruption is also a core principle in practices like Qi Gong and Reiki.
The infinity symbol has also been used as a visual tool in contemplative and spiritual teaching practices. Its continuous trace serves as a reminder that inner growth has no final destination, but is part of a constant process of evolution and return to oneself. When integrated into meditation or study spaces, it activates a symbolic field that inspires patience, balance, and connection with the eternal present.
The Power of the Infinity Symbol in the Expansion of Consciousness
Working with the infinity symbol can help deepen inner connection and open the path toward a broader perception of reality. Its fluid structure activates a state of consciousness that transcends the linearity of time, allowing access to experiences of unity and synchronicity. This expansion happens by recognizing that constant flow has no interruptions or limits.
In meditation, contemplating or visualizing the infinity symbol stimulates the balance between the brain’s hemispheres and facilitates a state of mindfulness. This internal balance is essential for experiencing a clearer, unfragmented perception and a greater integration of mind, body, and spirit. By tuning in to its frequency, a deeper understanding of personal purpose within the universal fabric is awakened.
The energy of infinity also drives us to let go of rigid thought patterns and open to the continuity of spiritual evolution. When used consciously, it becomes a powerful tool to align intention with the natural rhythm of existence. This experience allows the practitioner to access more subtle levels of consciousness and to feel a sense of belonging to the whole.
How to Use the Infinity Symbol in Spiritual Practices
The infinity symbol can be incorporated into various spiritual practices to activate states of inner balance, energetic continuity, and expanded consciousness. Its simple yet powerful form facilitates the integration of opposites and promotes harmony between body, mind, and spirit. Here are some ways to work with it:
- Conscious Visualization: Imagine the infinity symbol moving through your energy field. This practice helps harmonize the brain’s hemispheres and release mental blockages.
- Focused Meditation: Place an image of the symbol in front of you during meditation. Its continuous trace acts as a visual guide to center your attention and connect with the present.
- Energetic Tracing: Draw the infinity symbol in the air with your hand or with energetic crystals. This action can accompany healing rituals or vibrational rebalancing sessions.
- Cyclical Affirmations: Speak affirmations while visualizing the symbol’s flow. This technique enhances conscious repetition and aligns intention with spiritual expansion.
- Symbolic Decoration: Use the symbol on altars, in meditation spaces, or as a personal amulet. Its constant presence serves as a reminder of balance and energy continuity.
Differences Between the Infinity Symbol and Other Sacred Symbols
Although the infinity symbol shares elements with other sacred geometry diagrams, its message centers on continuous flow and the harmonic fusion of dualities. Each sacred figure has a unique purpose and activates different aspects of the self. Below are some key differences:
- Metatron’s Cube: Represents the totality of sacred geometric forms. Unlike the infinity symbol, its structure is more complex and focuses on the ordered manifestation of creation.
- The Merkaba: Functions as a vehicle for ascension and spiritual transformation. The infinity symbol, in contrast, relates more to continuous balance and interdimensional connection.
- The Seed of Life: Represents the beginning of creation from a central point. The infinity symbol expresses the perpetual movement of already manifested existence.
- The Flower of Life: Contains interconnected patterns revealing the structure of all creation. The infinity symbol is more abstract and dynamic, centered on endless flow.
- The Sri Yantra: Unites the masculine and feminine in a complex geometric diagram. Infinity also reflects duality, but through a unique form that flows in constant unity.
- The Vesica Piscis: Represents the intersection of two circles as a symbol of creation and unity. Unlike the infinity symbol, which flows without a crossing of planes, the Vesica Piscis expresses a meeting point where manifestation is born.
- The Torus: Shows a self-regulating energy flow in expansion and contraction. Unlike the torus, the infinity symbol represents that movement in a two-dimensional, cyclical path.
